In terms of the nn center-of-mass coordinates defined in equation
![]() we can rewrite equation
we can rewrite equation ![]() as
as
The polarization observables defined by equation ![]() can not be
easily related to the separate tensor components of the scattering matrix,
can not be
easily related to the separate tensor components of the scattering matrix,
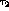 . Therefore, it is convenient to define a new set of spin
observables each of which depend on individual components of the scattering
matrix [BBW82].
. Therefore, it is convenient to define a new set of spin
observables each of which depend on individual components of the scattering
matrix [BBW82].
The new set of observables can be expressed as linear combinations of the polarization transfer observables defined above:
These observables are not independent quantities and are subject to the constraint

and are all non-negative: 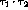 , where
, where 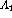 .
Using the definition of the polarization transfer coefficients (eqn.
.
Using the definition of the polarization transfer coefficients (eqn.
![]() ) and the standard expression for the scattering matrix (eqn.
) and the standard expression for the scattering matrix (eqn.
![]() ) one can derive expressions for the nn partial differential
cross sections which relate the spin observables,
) one can derive expressions for the nn partial differential
cross sections which relate the spin observables, 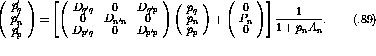 , to the
amplitudes of the M-matrix [IcK92]:
, to the
amplitudes of the M-matrix [IcK92]:
where I is the unpolarized differential cross section in the
center-of-mass frame. By inspection one can see that 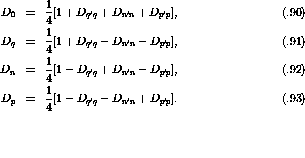 is related
solely to the piece of the interaction in the
is related
solely to the piece of the interaction in the  direction, or the
piece in which the spin is parallel to the direction of the momentum
transfer (referred to as
the longitudinal direction).
direction, or the
piece in which the spin is parallel to the direction of the momentum
transfer (referred to as
the longitudinal direction). 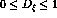 is related exclusively to a piece of
the interaction in the spin-transverse direction.
is related exclusively to a piece of
the interaction in the spin-transverse direction. 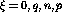 is also dependent
on a spin-transverse part of the reaction but not as simply as is the case
with
is also dependent
on a spin-transverse part of the reaction but not as simply as is the case
with  . The result is that a comparison of the spin-longitudinal and
spin-transverse parts of the nn interaction will come down to a comparison
of
. The result is that a comparison of the spin-longitudinal and
spin-transverse parts of the nn interaction will come down to a comparison
of 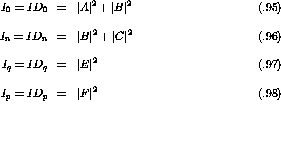 and
and 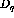 .
.