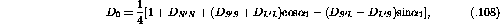 to be in terms of laboratory frame
polarization transfer observables.
to be in terms of laboratory frame
polarization transfer observables.
The nucleon-nucleon center-of-mass frame is ideal for deriving the
relations between spin observables and the interaction matrix, but it is
not always a useful way to conduct experiments. Intermediate energy
nuclear physics experiments are typically fixed target experiments,
so it is necessary
to convert the expressions for 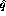 to be in terms of laboratory frame
polarization transfer observables.
to be in terms of laboratory frame
polarization transfer observables.
The laboratory frame will be defined as:

and

The axes are typically referred to as longitudinal 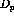 ,
normal
,
normal 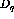 , and sideways
, and sideways 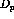 .
.
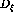 and
and
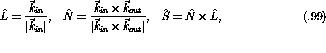 represent
right-handed Cartesian coordinate frames [BBW82]. In terms of the
laboratory frame coordinates equation
represent
right-handed Cartesian coordinate frames [BBW82]. In terms of the
laboratory frame coordinates equation
![]() can be expressed as [Che93]
can be expressed as [Che93]
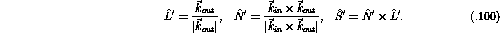
The analyzing power associated with the out-of-plane component 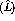 is
still referred to as
is
still referred to as 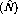 by convention. Therefore, the laboratory frame
polarization observables can be obtained by measuring both the initial and
final polarization.
by convention. Therefore, the laboratory frame
polarization observables can be obtained by measuring both the initial and
final polarization.
In order to determine the Bleszynski, et al. observables, 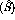 ,
[BBW82] it is necessary to express the laboratory frame observables
(i.e.
,
[BBW82] it is necessary to express the laboratory frame observables
(i.e. 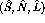 ) in terms of the center-of-mass spin observables
(i.e.
) in terms of the center-of-mass spin observables
(i.e. 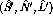 ). This requires a transformation of the reference frame
which includes a relativistic effect on the spin rotation. This
transformation is presented in detail by [IcK92].
). This requires a transformation of the reference frame
which includes a relativistic effect on the spin rotation. This
transformation is presented in detail by [IcK92].
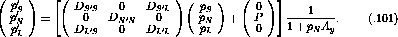
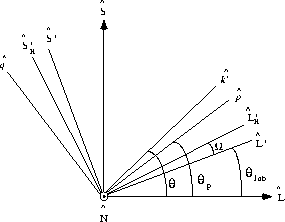
Figure: Scattering kinematics in the center-of-mass and laboratory
reference frames including the relativistic effect on the spin rotation
explicitly [IcK92].
First of all, the unit vector normal to the scattering plane will remain
unchanged 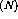 , so
, so 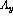 .
For the in-plane components the final state coordinates,
.
For the in-plane components the final state coordinates, 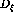 and
and 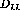 , will be rotated by an angle,
, will be rotated by an angle, 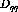 , which is the
relativistic spin rotation as is shown in figure
, which is the
relativistic spin rotation as is shown in figure ![]() .
.
 is given by
is given by

where 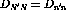 is the velocity of the particle,
is the velocity of the particle, 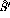 is the
velocity of the c.m. frame with respect to the laboratory frame,
is the
velocity of the c.m. frame with respect to the laboratory frame,
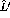 , and
, and  and
and 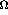 are the
scattering angles in the c.m. and laboratory frames, respectively.
If we take
are the
scattering angles in the c.m. and laboratory frames, respectively.
If we take 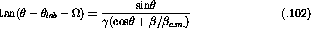 to be the angle between the incident beam direction,
to be the angle between the incident beam direction,
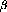 , and the unit vector
, and the unit vector 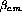 as defined in equation
as defined in equation
![]() (see fig.
(see fig. ![]() ) then the transformations look like
) then the transformations look like




Given these expressions between the coordinates the relations between in-plane spin observables is
where 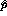 .
Using equation
.
Using equation ![]() , equations
, equations ![]() to
to ![]() can be
rewritten as [Lut93]
can be
rewritten as [Lut93]
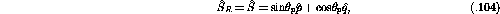
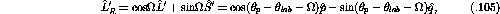
where
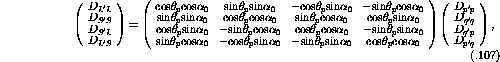
Note: It is also possible to define 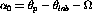 as [Che93]:
as [Che93]: