Understanding detectors
Let us now return to the process of detecting an electron.
We start again with an electron waveform with two well-separated bumps: one on the left and one on the right.
To locate the electron, we had used a pair of detectors: one near the left bump and one near the right bump. But we have already seen from our earlier experiments that only one of these detectors will detect an electron. So to simplify matters, let us just use a detector near the left bump. We will then find the following:
- There is a \( 50\%\) probability that the muon in the detector rises to the top; i.e., the detector finds an electron at the left bump.
- There is a \( 50\%\) probability that the muon in the detector stays at the bottom; i.e., the electron in on the right.
- There is no way for us to predict which of these possibilities will occur in given measurement; all we can say is that if we repeat the experiment many times, we can deduce the above mentioned probabilities.
It may seem from this that physics is unpredictable; i.e., there are no definite laws that take us from a given initial state to a later final state. If this were the case, we would say, as Einstein did, that 'God plays dice with the world, and decides the outcome of a measurement by what the dice do'. But we will now see that such is not the case. There is a well defined law which predicts the evolution of states; the seeming randomness is arising from what we call a 'detection' or 'measurement'.
A 2-particle system
It may seem that in the experiment above, we are looking at one particle - the electron. But the crucial point is that that we really have to focus on two particles: the electron that we started with, and the muon that we use to detect the presence of this electron. Since these particles interact, we will get an entangled state of these two particles. Thus we cannot consider separate wavefunctions for the electron and the muon.
We proceed as follows:
- We draw an axis labelled \( x \) to describe the position of the electron. Positive values of \( x\) correspond to the electron being on the right, and negative values of \( x \) correspond to the electron being on the left.
- We draw an axis labelled \( z \) to describe the position of the muon. (The muon wave moves in an up-and-down direction, and the symbol \( z\) is often used for this vertical direction.) Values of \( z \) near zero (i.e., the bottom of the depicted region) correspond to the muon being at the bottom of the cylinder. Values of \( z \) near the top correspond to the muon being at the top of the cylinder.
- The electron-muon system is described by a waveform over this 2-dimensional \( x-z\) plane.
The electron-muon waveform
We now describe the behavior of this waveform for the experiment in fig.1.
- At the start, the electron wave is equally on the left and on the right. The muon starts at the bottom of the cylinder. Thus the waveform has a bump in the bottom left corner and a bump in the bottom right corner.
- Now we come to the interaction of the electron with the detector. If the electron is on the left, then it will push the muon up. So after a while, we should find a bump in the top left corner: the electron is on the left, and the muon has been correspondingly pushed to the 'up' position.
- There was also a probability for the electron to be on the right. If this is the case, then the muon in our left detector should not be pushed up. So we continue to have a bump in the bottom right corner: the electron is on the right, and the muon is at the bottom.
God does not play dice
To summarize, the wavefunction of the 2-particle system starts as in fig.1, and ends as in fig.2. The full evolution of this wavefunction between the initial and final times is given in fig.3.
We can now state the crucial point about the detection process:
The evolution of fig.3 is completely determined by the rules of wave-mechanics, and is the same each time we repeat the experiment.
Thus when we look at the full system - the electron as well as the muon - then a definite physical rule tells us how to go from the initial state to the final state. In this sense, 'God does not play dice'.
Summary
This observation is very significant. The randomness of experimental outcomes had suggested that physics may not be predictable. Now we see that is we look at everything - the electron as well as the detector muon - then the overall wavefunction describing this total system has a completely predictable evolution. Each time we do the same experiment, we will be starting with the same initial wavefunction for this total system, and we will get the same final wavefunction as well. The details of the evolution can be found by the rules of wave mechanics applied to the wave on the 2-dimensional space \( x_1, x_2\).
Given this, our next question is: what is the source of the randomness observed in our experiment?

The electron is taken to have an initial waveform consisting of two equal and well-separated bumps.

We place a detector on the left only; if the detector sees an electron then the electron is on the left, and if it sees no electron then the electron is on the right.
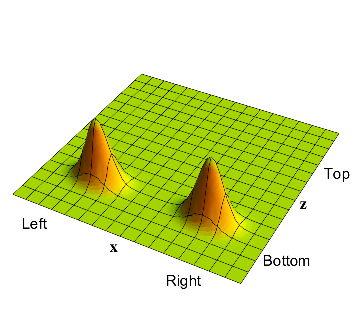
The full wavefunction of the electron+muon system at the start of the experiment: the bump in the bottom left corner describes the electron on the left and the muon in the down position, and the bump on the right describes the electron on the right and the muon again in the down position.
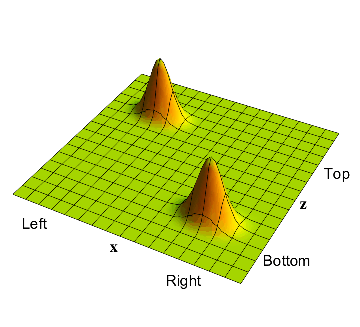
The full wavefunction of the electron-muon system after the detection process. The part where the electron was on the left now has the electron on the left and the muon in the up position. The part where the electron was on the right has the electron on the right and the muon still in the down position.
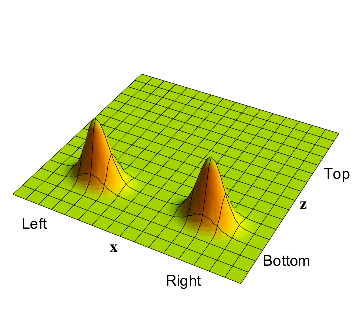
The full evolution of the wavefunction from its initial shape to its final shape. This evolution is the same each time we repeat the experiment; in this sense 'God does not play dice'.