The source of randomness
We have seen that the overall wavefunction describing the system and the detector has a predictable behavior: each time we repeat the experiment we will get the same evolution for this total system. We can ask: where does the randomness seen in our experiment come from?
The answer is that the randomness arises when we look not at the whole system - the electron and the muon - but only at one part of the system - the electron. More precisely, in the process of detection, we try to see the state of the electron from the viewpoint of the detector particle, i.e., the muon.
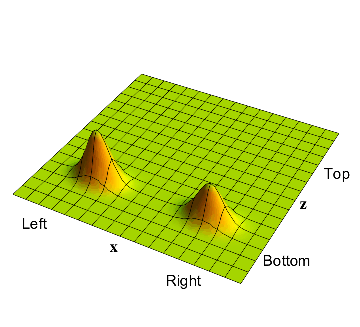
From fig. 3 we see that the muon does not see a definite position for the electron. There is a \( 50\%\) chance that the muon sees the electron on the left - this is the bump in the top left corner. There is also a \( 50\%\) chance that the muon sees the electron as being on the right - this is the bump in the bottom right corner.
Thus the state of the muon is itself split among two possibilities, and so the muon cannot 'say' with definiteness what the electron is doing. The detector therefore just sees a probability \( 50\%\) that the electron is on the left and a probability \( 50 \%\) that the electron is on the right.
The utility of measurement
At this point one might wonder if there was any point is using the muon to detect the electron. If the state of the muon itself splits into two possibilities, then perhaps this detection process was meaningless?
Such is not the case. The important point is that even though the muon does not have a definite answer for where the electron is, it does have a correct correlation with the position of the electron.
In detail, this means the following. When the muon thinks the electron is on the left, then it rises up. When the muon thinks the electron is on the right, it does not rise up. These are the two bumps in fig. 2. But there are no bumps in the 'incorrect' locations. Thus there is no bump in the bottom left corner, which would describe an electron on the left and a muon that failed to be repelled to the top. Similarly, there is no bump in the top right corner, which would describe an electron on the right and the muon in our left detector rising up. Thus after interacting with the electron, the position of the muon always corresponds to 'correctly correlated' situations.
Summary
Let us summarize the overall situation with the help of an example.
- We take an electron with the waveform in fig.1: there are two bumps, with the left bump having more strength than the right.
- We square this waveform, getting the graph in fig.2. The total area under this squared curve is unity, as it must be. The left bump has area \( 2/3\) and the right bump has area \( 1/3\).
- We now ask: is the electron on the left or on the right? To answer this question we place a detector on the left and a detector on the right. containing a muon. If the muon is repelled up, we will say the electron is on the left; if it does not rise up, we will say that the electron is on the right.
- The full system of the electron and muon is described by a wavefunction on a 2-dimensional plane \( x-z\). At the start of our experiment the muon is in the down position. Thus the starting shape of this wavefunction is as given in fig. 3. The bump in the bottom left corner corresponds to the electron on the left and the muon in the down position. The bump in the bottom right corner corresponds to the electron on the right and the muon again in the down position. The volume under the first of these bumps is \( 2/3\) and under the second is \( 1/3 \).
- This overall wavefunction has a definite evolution given by wave-mechanics; there is nothing random about its evolution. In this sense, 'God does not play dice'. The evolution is given in fig. 4. The bump in the left hand corner moves to the top left corner, signaling that the muon has been repelled to the up position if the electron was on the left; i.e. near the detector.
- In a measurement process, however, we are forced to see the electron from the viewpoint of the detector particle, the muon. Thus we do not see the full system of the electron and muon; i.e., we do not have the perspective which is described by the overall wavefunction. The measurement is pictured in fig. 5. If we repeat the experiment many times, we find that the detector behaves with randomness. With a probability \( 2/3\) the muon rises up, and with a probability \( 1/3\) it does not. These fractions correspond to the volumes under under the left and right bumps in the overall wavefunction of fig. 4. They are also the fractions describing the bumps of fig.2, so we see why fig. 2 is called the probability graph of the electron.
- Note that the muon is always 'correctly correlated' with the electron, so the measurement process never gives an answer that is inconsistent with physical law. Lastly, the situation cannot be improved by making a 'better' detector. Whatever detector we take, it remains true that the overall wavefunction of electron+detector will have an evolution that is completely determined by wave mechanics. But seen from the viewpoint of the detector, the electron position can be described only in terms of probabilities, so that the outcome of any one measurement remains random.
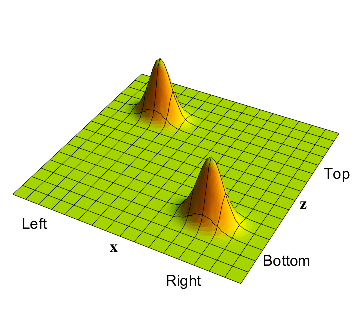
After the detection process, the overall wavefunction of the electron-muon system has two bumps: one corresponding to the electron on the left and the muon in the 'up' position and one corresponding to the electron on the right and the muon in the 'down' position.
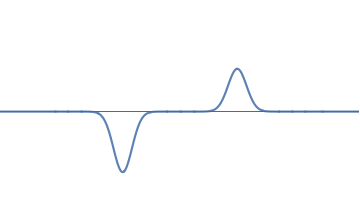
2(a): We start with this electron wavefunction
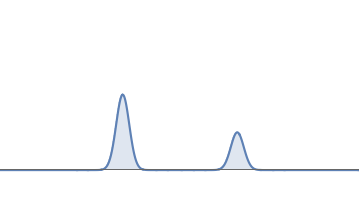
2(b): Squaring gives the probability graph; the area is \( 2/3\) on the left and \( 1/3\) on the right.
2(c): The evolution of the overall wavefunction is the same, each time the experiment is repeated.

2(d): Measurement however sees the result from the viewpoint of the muon; \( 2/3\) of the time the muon will rise (signaling an electron on the left) and \( 1/3\) of the time it will not.