Stacking waves
We have seen that the electromagnetic wave has a smallest unit - the photon; we cannot have half a photon. The electron wave is also discrete, so that we can have one electron but not half an electron.
We can however have an electromagnetic wave with the strength of two photons. We can think of such a wave as two photons stacked on top of each other to give a wave of twice the energy.
It turns out however that we cannot stack two electron waves on top of each other to make an electron wave with twice the strength.
This may look strange: why should photon and electron waves behave differently? But as we will now see, this difference in stackability of part of a general principle, which applies to all waves.
Spin
Each fundamental entity - photon, electron, etc. - is characterized by a number called its spin. Examples are:- The Higgs particle: spin \( 0\)
- Electron, proton, neutron: spin \(\frac {1}{2} \)
- The photon: spin \( 1 \)
The spin is a very quantum feature, but a rough picture in classical terms is the following. Think of the entity as a classical particle. This particle can spin about its own center, and the amount of this spin will be described by an angular momentum \( S \). This angular momentum can only take discrete values:
We therefore get two categories of particles:
- Bosons: These are the particles for which the number \( s\) is an integer; i.e., \( s=0,1,\dots \). The waves for these particles can be stacked to make waves that are stronger than the minimum wave by a factor \( 2,3, \dots \).
- Fermions: These are the particles for which the number \( s\) is a half-integer; i.e., \( s=\frac{1}{2},\frac{3}{2},\dots \). The waves for these particles cannot be stacked to make waves that are stronger than the minimum wave.
Thus if we consider a given shape of wave at a given place, then there can be \( 0 \) electrons with that waveform or \( 1\) electrons with that waveform, but there cannot be two electrons with that waveform. This fact is called the Pauli exclusion principle.
The above properties of bosons and fermions show up in a remarkably diverse set of phenomena. Let us note some examples.
The behavior of bosons
When we stack a large number \( n \) of boson waves on top of each other, then we say that we have made a coherent state of the bosons. Conversely if the available energy is spread over many bosons at different places (i.e. they are not stacked to make stronger waves) then we say that we have an incoherent state.- Radio waves: These are coherent states. These waves have a large wavelength \( \lambda \), so the energy of a single photon is very small. But because a large number of photons are stacked to make the wave, we can detect it readily with a radio set.
- Light bulb: The filament in the bulb emits a large number of photons, but each photon is emitted by a different atom, and so the light in incoherent.
- Laser: A laser beam can have the same wavelength and the same power as the light from the light bulb, but all the photons are in a coherent state; i.e. they are stacked on top of each other. The coherent nature of the beam allows it to cut through metal, something that the light from the bulb cannot do.
The behavior of fermions
The Pauli exclusion principle says that we cannot stack together many electrons having the same waveform. This fact has a very interesting implication for the behavior of all matter.
Consider a heavy weight placed on a rock. Why does the rock not collapse under this weight?
If atoms were solid balls, we could imagine that each layer of atoms in the rock is supported by the layer of atoms under it, and so on till the center of the earth. But the objects making the atoms - electrons, protons and neutrons - are all waves. Why does the wave in one atom not descend down to the layer below and join the waves in that layer? If it did, then all the layers of rock would collapse to a very thin layer; i.e., the rock would not be able to resist any weight at all.
The reason that there is no such collapse is the Pauli exclusion principle. If the electrons in one layer moves down to the layer below, then we would have an two electron waves of the same form at the same place. But such 'stacking' is not allowed for electrons by the Pauli exclusion principle; we can have at most one electron with a given waveform. So the atoms cannot overlap, and the rock does not crush.
It is interesting that the strongest forces that cause matter to resist compression come from the Pauli exclusion principle. In particular white dwarfs and neutron stars resist collapse under the tremendous pressure of their own gravity because of the Pauli exclusion principle applied to electrons and neutrons respectively. When the gravity is strong enough to overcome even this pressure, the star collapses to a black hole.
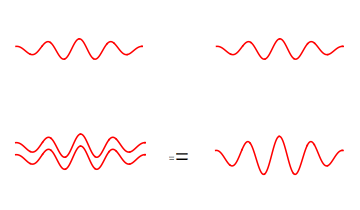
We can have two separate photons at different places, or join them to a photon with twice the energy.
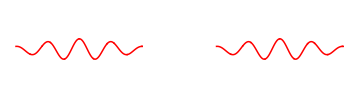
We can have two separate electrons at different places, but we cannot join them to make an electron wave with twice the energy.