The discreteness of the electron wave
Electrons are discrete: we can have one electron but not half an electron. How is this fact encoded in the wave describing the electron?
Suppose we have a wave that describes an electron. We should be able to change the shape of the wave, but we should not be able to make it weaker. The total strength of the wave should be unity in some sense, expressing the fact that we have one electron.
Defining the strength of the electron wave
We proceed as follows- Consider an electron wave. The height of the wave at any place can be described by a number. This number can be positive or negative.
- Square this number at each place, getting a new graph. Note that the height of this new graph will not be negative anywhere.
- Find the area under this squared graph. For an allowed electron wave, this area must equal \( 1 \).
We can see that these steps make intuitive sense. The electron wave has a large strength when it has a large height, whether this height is positive or negative, Squaring the height gives a positive strength for both these cases. The area under the squared graph involves not only the height but also the width of the wave; thus a wave stretching over a longer distance will be attributed a larger strength.
Some notation
We note here some commonly used symbols used in describing the electron wave. (We will not, however, need these mathematical details for our understanding of the basic principles of quantum mechanics.)
- Consider electron waves in one dimension. We label the points along this direction by their coordinate \( x \).
- The amplitude of the electron wave (i.e. the wave height) is typically denoted by the symbol \( \psi \). Thus the wave is described by a function \( \psi(x) \).
- The square of the amplitude is typically denoted by the symbol \( P \), for reasons that we will see later. Thus we get a function \( P(x) \).
- We have considered \( \psi \) as a real number. However, \(\psi \) is in general allowed to be a complex number:
\[ \psi~=~\psi_1 ~+~i\, \psi_2 \]
Thus taking \( \psi(x)\) to be a real function is a special case. However we will continue to sketch \( \psi(x) \) as a real function, since this will be sufficient for understanding the principles of quantum theory.
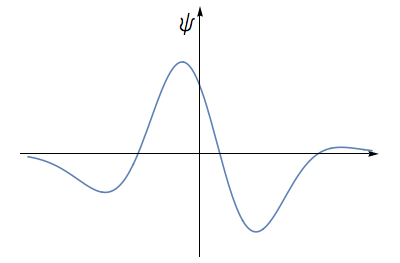
The electron waveform can take both positive and negative values.
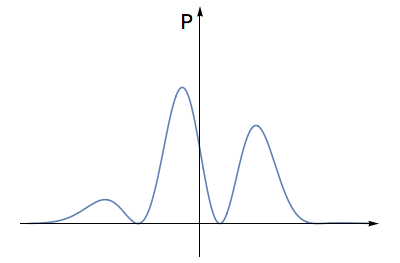
Squaring this waveform gives a graph that is not negative anywhere.
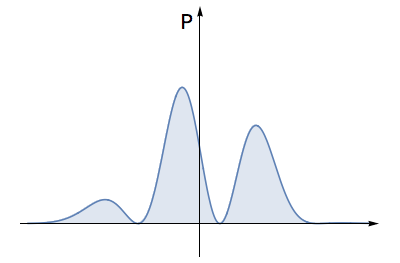
The total area under this squared graph must equal \( 1 \). This means that the wave has strength 'unity', and describes one electron.