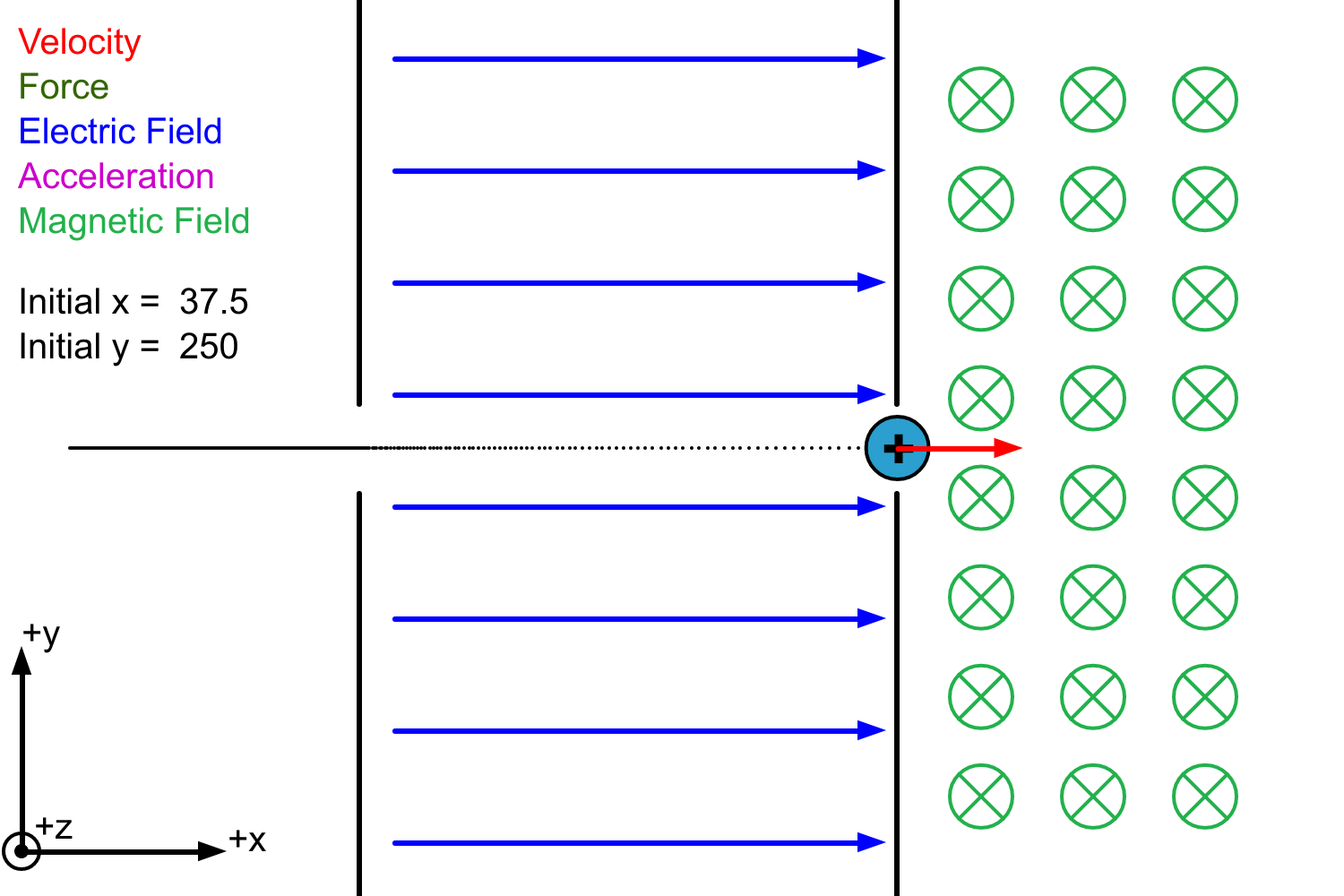
You may recall the last programming exercise that involved a particle being accelerated through two charged plates. In this exercise we will add a magnetic field to the right hand side of the simulation. The particle only experiences this field when it passes into the right-hand side. This example is loosely based on the idea of a "mass spectrometer". It turns out that if you vaporize a little bit of a sample with some unknown molecules there tends to be alot of molecules that lose ONE electron. Since the molecule has lost an electron it has a +1 charge. The mass of the molecule is essentially the same even if it is missing an electron because electrons make up a very, very small fraction of the mass of atoms. As you will learn about in this lab, the trajectory of the particle in the magnetic field tells us something about the mass of the particle (if you already know q, v, and B for example).
Advice: For some reason the simulation this coding activity produces looks better in chrome than it does in firefox or other browsers. It still works fine in all browsers! but you may notice that the + signs aren't in exactly the midle of the particle. Sorry.
Step 1. Check out the modified version of the earlier programming lab by clicking on this link. As you can see there is a magnetic field pointing into the page on the right hand side. The positively charged particle does *not* react to this magnetic field simply because no one has told the program what to do when a magnetic field is present! Your task will be to tell the program what to do in this case.
Step 2. Open up the bfield code in an editor
Click on this link to open the bfield code in a p5.js editor
Important! Create an account with the editor or sign in to an existing account. Then click "Duplicate" so you can have your own version of the code.
Note: You cannot use your code from earlier exercises because those exercises don't have the capability to draw the magnetic field, and there are a few other minor formatting differences.
Step 3. Before doing any coding, what is the direction of the magnetic force on the positive charge when it enters the magnetic field as shown below? (Hint: The B field is into the page instead of out of the page as in the previous diagram.)

Step 4. What happens later on, after the charge has been deflected? What should the overall trajectory qualitatively look like and why? Write down what your expectation is in what you turn in for this lab. It's ok if your expectation turns out to be wrong. You won't lose any points.
Step 5. (You don't really have to do anything for this step except to try and understand the conclusion.) On the right hand side of the simulation, the only force the charge feels is the magnetic force. Since this is the only force this means that if we can figure out the x and y components of the magnetic force then we can figure out the x and y acceleration: $$F_{\rm netx} = \sum F_x = F_{{\rm mag},x} = m a_x$$ $$F_{\rm nety} = \sum F_y = F_{{\rm mag},y} = m a_y$$ $$\vec{F}_{\rm mag} = q \, \vec{v} \times \vec{B}$$
In Physics 1251 we often write that the magnitude of the magnetic force is this: $$ F_{\rm mag} = | \vec{F}_{\rm mag}| = q |\vec{v}| \, |\vec{B}| \sin \theta = q v B \sin \theta$$ where $\theta$ is the angle between the velocity and the magnetic field. In this case, the angle between the velocity vector and the magnetic field is always 90 degrees (think about why this is true) which means that the magnitude of the magnetic force is just this: $$F_{\rm mag} = q v \, B = q \sqrt{v_x^2 + v_y^2} \, B $$
This equation is great except that what we really need is $F_{{\rm mag},x}$ and $F_{{\rm mag},y}$. Ultimately, we will find that the following is true: $$F_{{\rm mag},x} = q v_y B$$ $$F_{{\rm mag},y} = -q v_x B$$
For example, notice that $F_{\rm mag} = \sqrt{F_{{\rm mag},x}^2 + F_{{\rm mag},y}^2} = q \sqrt{(-v_x)^2 + v_y^2} \, B = q \sqrt{v_x^2 + v_y^2} \, B$ as expected.
Here is the formal derivation of $F_{{\rm mag},x}$ and $F_{{\rm mag},y}$ :
If you look carefully at the picture, you'll realize that $\vec{B} = B_o \hat{z}$. The velocity is always $\vec{v} = v_x \hat{x} + v_y \hat{y}$. The cross product is therefore, $$\vec{v} \times \vec{B} = (v_x \hat{x} + v_y \hat{y}) \times (B_o \hat{z}) = v_x B_o (\hat{x} \times \hat{z}) + v_y B_o (\hat{y} \times \hat{z})$$
According to the right hand rule, $\hat{x} \times \hat{z} = -\hat{y}$ and $\hat{y} \times \hat{z} = \hat{x}$. This means that $\vec{F}_{\rm mag}$ is
$$\vec{F}_{\rm mag} = q \vec{v} \times \vec{B} = q v_x B_o (-\hat{y}) + q v_y B_o (\hat{x})$$
Which is equivalent to
$$F_{{\rm mag},x} = q v_y B_o$$
$$F_{{\rm mag},y} = -q v_x B_o$$
Step 6. Now that I have given you $F_{{\rm mag},x}$ and $F_{{\rm mag},y}$ you can solve for $a_x$ and $a_y$. Go ahead and solve for these accelerations and write down your result for $a_x$ and $a_y$ in what you submit for the lab.
Now for the coding part. Using the accelerations you just calculated you can figure out the change in velocity over the time interval $\Delta t$. $$\Delta v_x = a_x \Delta t$$ $$\Delta v_y = a_y \Delta t$$
Use your expressions for $\Delta v_x$ and $\Delta v_y$ in your code. Use these expressions inside of the if statement that has the code for when the particle is inside the magnetic field. I'm talking about this section of the code:
if ( x > x_plate_right )
{
deltaVx = 0.0; // change in vx from magnetic field
deltaVy = 0.0; // change in vy from magnetic field
}
When finished your code should behave like this
Step 7. The "gyroradius"
As you saw in Step 5., particles that move into a magnetic field make a circular path. The radius of the circular path is called the "gyroradius".
Use the initial and final positions of the particle to get a number for the radius of the circular path that the particle makes in your simulation. This radius is often called the "gyroradius".
There is a clever way of thinking about the magnetic force that allows us to come up with a formula for how that radius (a.k.a. the "gyroradius") depends on the speed, mass, and charge of the particle, as well as the strength of the magnetic field. Your physics textbook probably talks about the "gyroradius" formula, so feel free to look that up. Here is the basic idea.
In Step 5 we talked about $F_{{\rm mag},x}$ and $F_{{\rm mag},y}$ which are the x and y components of the magnetic force. But if all you care about is the magnitude of the magnetic force, the equations get much simpler. In Step 5 we had this formula:
$$F_{\rm mag} = q vB$$
where $v$ is the speed of the particle and $B$ is the absolute value of the magnetic field (this is important because the magnetic field in this case is negative, into the page, whereas we are just calculating the magnitude of the magnetic field, which either positive or zero).
In Step 6 we learned that the speed of the particle is roughly the same even as the particle changes direction. If you decreased dt from 0.1 to smaller and smaller values you will find that you get closer and closer to the initial speed. This is a sign that that in real life the speed doesn't change at all! So $v$ = constant and since q and B are constants, this means that $F_{\rm mag}$ = constant.
Aside: You can see from the program that $F_{\rm mag}$ = constant because the magnetic force arrow changes direction (always pointing to the center of the circle) but it doesn't get longer or shorter, which would indicate a change in the magnitude of the magnetic force.
A constant force like this will move the particle in a circle with a constant acceleration $a_{\rm circ} = v^2 / r$ because everything that moves in a circle has that acceleration.
Putting this all together we get:
$$F_{\rm mag} = m a_{\rm circ}$$
$$q v B = m \frac{v^2}{r}$$
Solve for r in the expression above and remember that B is the absolute value of the magnetic field, which is important for making sure that r > 0. Then use your equation to calculate a value for r and see if it matches up with the radius of the circle in the program. This radius is often called the "gyroradius". How well does your calculation for the gyroradius compare to the gyroradius measured from the simulation? Remember that the units here are simplified here so you can just use the known values for q, v, B, and m in the program to do this calculation like you did in the particle accelerator exercise. You should get better than +/- 10% agreement between your calculation and the measurement from Step 7a. (Note: you might be able to get better agreement with a smaller dt value).
Step 8. What about protons?
The program assumes that we are accelerating a Deuteron (q = +1, mass = 2). Would a proton (q = +1, mass = 1) have a larger or smaller gyroradius than a Deuteron? Why?
Step 9. Change the charge from +1.0 to -1.0 and change the electric field from positive to negative and see if the particle moves in the magnetic field the way you expect (which way do you expect?!). Just for fun, edit bfield.js so that the picture is of a negatively charged particle.
Do this by changing
positive(x,y);to
negative(x,y)
And make sure to change the electric field from positive to negative, or else the negatively charged particle may not make it through! What happens?!
1. State which direction that the magnetic force will exert on the particle (Step 2)
No calculation necessary. When the particle enters the region with the magneitc field, will the magnetic force on the particle be up, down, left, right, into or out of the page? The direction of the magnetic force needs to be correct for you to get full credit on this question
2. Guess what the trajectory of the particle will look like in the magnetic field (Step 3)
No calculations necessary. Just guess qualitatively what will happen to the particle when it enters the magnetic field. Will it go straight, up, down, in a circle, etc.? It's ok if you guess wrong. As long as you think about it and give your best guess. Justify your answer (with words) for full credit
3. Write down what you should use for $a_x$ and $a_y$ in the the comments accompanying your code (Step 5)
Look carefully at the end of Step 4 and use this information to figure out what you should use for $a_x$ and $a_y$ (hint: divide by mass). Write down $a_x$ and $a_y$ in the comments and implement this in the code (don't forget $\Delta t$!).
4. Check if the velocity at the end of the simulation is about the same as it would be if there were no magnetic field (Step 6)
In the comments for the code write down the final velocity of the particle in the simulation with the magnetic field. Then either set B = 0 or go back to your earlier simulation and check the final velocity is and write this down in your comments. It's ok if these are off by +/-10%. More than that could indicate a problem.
5. Measure and calculate the gyroradius (Step 7)
Write down your calculated gyroradius and the measured gyroradius. The two should be consistent within 10-20%. More than that could indicate a problem.
6. What would happen to a proton compared to a Deuteron (Step 8)
7. Which direction would a negatively charged particle move in the magnetic field? (Step 9)
Change the charge from +1 to -1, change the E field to a negative value and see what happens when the particle enters the magnetic field. Write down what happened.