


Next: The time direction
Up: Uncertainties and resolution
Previous: Uncertainties and resolution
In the following, we attempt to understand the resolution
in the direction along the padrow, so as to
correctly estimate the position uncertainty hit-by-hit.
The first term in Equation 9 does not depend on crossing
angles and only on the signal:noise and signal shape. To evaluate whether
the hitfinder estimates this component of the uncertainty correctly, we
generated low-track-density toy events, in which tracks cross the padrow
with zero crossing angle. The field was turned off (in this simulation,
this did not change the transverse diffusion from its field-on value) so
that highly ionizing particles as well as m.i.p's would provide straight
tracks. Then, the electronics noise in the simulator was varied and the
resolution studied. ``100%''
noise was the nominal noise: 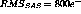 ,
, 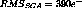 .
RMS resolutions and uncertainties are shown in Figure 22
as a function of noise.
There, it is seen that the hitfinder slightly overestimates the uncertainty
from the first term of Equation 9. This is understood
to be the consequence of using Equation 8, which is based
on an idealized assumption of infinite shaping time, to calculate the
uncertainty on pad projections.
.
RMS resolutions and uncertainties are shown in Figure 22
as a function of noise.
There, it is seen that the hitfinder slightly overestimates the uncertainty
from the first term of Equation 9. This is understood
to be the consequence of using Equation 8, which is based
on an idealized assumption of infinite shaping time, to calculate the
uncertainty on pad projections.
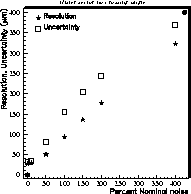
Figure 22: Simulated  =0 tracks passed through the slow simulator with
varying levels of noise are used to study resolution and calculated
uncertainties. The amount of noise is quantified in terms of the
nominal electronics noise in the default simulator. Note that resolution
and uncertainty do not vanish at ``% noise''=0, because the effective
noise introduced by digitization is not removed.
=0 tracks passed through the slow simulator with
varying levels of noise are used to study resolution and calculated
uncertainties. The amount of noise is quantified in terms of the
nominal electronics noise in the default simulator. Note that resolution
and uncertainty do not vanish at ``% noise''=0, because the effective
noise introduced by digitization is not removed.
Figure 23
shows that, for each noise value, the resolution
scales as expected with signal size: resolution increases linearly with
the inverse of the signal size, 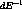 .
.
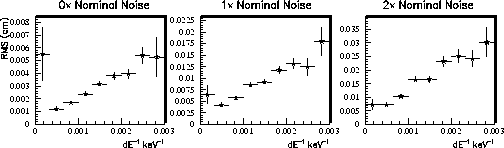
Figure 23: The dependence of the resolution (RMS of the residual distribution)
is seen to show a linear dependence on the inverse of the hit size
for simulated  =0 tracks, for all values of noise. Note the scale
change for resolution as the noise increases.
=0 tracks, for all values of noise. Note the scale
change for resolution as the noise increases.
Having established that the resolution due to the first term in
Equation 9 is understood and well-estimated by the
hitfinder code, we turn to tracks with finite crossing angle.
The slow simulator currently does not incorporate finite electron
effects, so the second term in Equation 9
is not expected to contribute to the resolution ( =0)
[9]. The third term, which arises from
fluctuations in energy loss as a track crosses the padrow at non-zero
angle, will increase the resolution strongly. The resolution in the
outer sector from a Au-Au event is shown in Figure 24
as a function of crossing angle
=0)
[9]. The third term, which arises from
fluctuations in energy loss as a track crosses the padrow at non-zero
angle, will increase the resolution strongly. The resolution in the
outer sector from a Au-Au event is shown in Figure 24
as a function of crossing angle  .
.
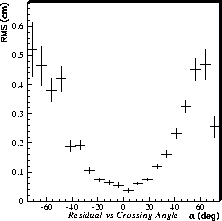
Figure 24: Resolution as a function of padrow crossing angle is shown
for the outer sectors in a simulated Au+Au event.
A series of low-multiplicity events were run through the slow simulator,
with varying vertex position (in order to study seperately effects of
crossing angle  and drift length L), and varying electronic noise.
The
RMS of the residual distribution was calculated as a function of
and drift length L), and varying electronic noise.
The
RMS of the residual distribution was calculated as a function of  ,
dE/dx, L,
,
dE/dx, L,  , and noise level.
No dependence of the padrow spatial resolution was seen as a function of
, and noise level.
No dependence of the padrow spatial resolution was seen as a function of
 or L, as expected since
or L, as expected since  =0 (see above).
The dependence of the RMS on
=0 (see above).
The dependence of the RMS on  and signal size is shown in the
case of zero electronics noise in
Figure 25. The worsening of the resolution with crossing
angle is clear, as is the fact that the rate of this worsening is greater
for large hits (large dE/dx) [9].
and signal size is shown in the
case of zero electronics noise in
Figure 25. The worsening of the resolution with crossing
angle is clear, as is the fact that the rate of this worsening is greater
for large hits (large dE/dx) [9].
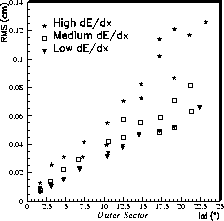
Figure 25: Observed resolution (RMS of residual distribution) for
low-multiplicity events with zero electronics noise is shown as
a function of the crossing angle alpha, with cuts on dE/dx of the hit.
Equation 9 contains two constants, 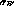 and
and 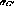 , which depend only on the chamber geometry and
gas properties [9]. (The primes on the constants
are in part to distinguish them from similar ``constants'' used elsewhere
[6,7,10] which depend on hit properties.) These constants
must be determined empirically. We find using P-10 gas for the outer sector
, which depend only on the chamber geometry and
gas properties [9]. (The primes on the constants
are in part to distinguish them from similar ``constants'' used elsewhere
[6,7,10] which depend on hit properties.) These constants
must be determined empirically. We find using P-10 gas for the outer sector
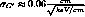 and for the
inner sector
and for the
inner sector 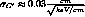 .
.
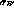 will be determined after TSS is updated.
We note that the values for
will be determined after TSS is updated.
We note that the values for 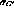 may also change
if, for example, the energy loss gets calculated differently.
may also change
if, for example, the energy loss gets calculated differently.
The tracker, with 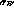 and
and 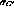 in hand,
and a hypothesis of
in hand,
and a hypothesis of  , can accurately estimate the uncertainty
of the hit position, as is shown in Figure 26, where the
uncertainties estimated by
a tracker using the form 9 are compared for the range
of hit classes to the rms of the residual distribution for that hit class.
, can accurately estimate the uncertainty
of the hit position, as is shown in Figure 26, where the
uncertainties estimated by
a tracker using the form 9 are compared for the range
of hit classes to the rms of the residual distribution for that hit class.
As numerical examples of the resolution in the x- and y- directions,
we note that, averaging over all particles in a Au+Au event,
the Gaussian widths of the residual distribution
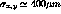 , whereas for those hits whose parent
tracks had
, whereas for those hits whose parent
tracks had 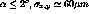 . It is this
small
. It is this
small  resolution that scales as signal:noise.
resolution that scales as signal:noise.
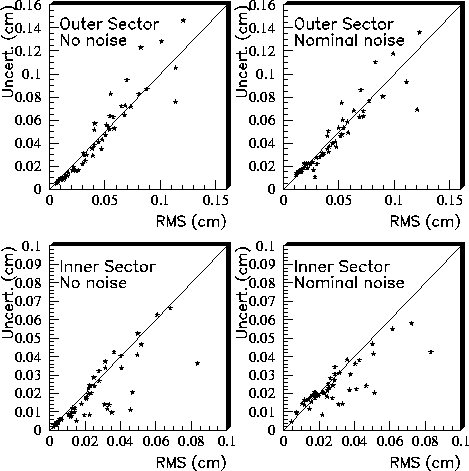
Figure 26: Estimated uncertainty in the
position along the padrow that would be calculated by
a tracker is compared to the position resolution for inner and outer
sector, for two values of electronic noise. 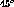 lines are drawn for
reference.
lines are drawn for
reference.



Next: The time direction
Up: Uncertainties and resolution
Previous: Uncertainties and resolution
Michael A. Lisa
Tue Feb 6 15:49:35 EST 1996
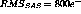 ,
, 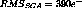 .
RMS resolutions and uncertainties are shown in Figure 22
as a function of noise.
There, it is seen that the hitfinder slightly overestimates the uncertainty
from the first term of Equation 9. This is understood
to be the consequence of using Equation 8, which is based
on an idealized assumption of infinite shaping time, to calculate the
uncertainty on pad projections.
.
RMS resolutions and uncertainties are shown in Figure 22
as a function of noise.
There, it is seen that the hitfinder slightly overestimates the uncertainty
from the first term of Equation 9. This is understood
to be the consequence of using Equation 8, which is based
on an idealized assumption of infinite shaping time, to calculate the
uncertainty on pad projections.

 =0 tracks passed through the slow simulator with
varying levels of noise are used to study resolution and calculated
uncertainties. The amount of noise is quantified in terms of the
nominal electronics noise in the default simulator. Note that resolution
and uncertainty do not vanish at ``% noise''=0, because the effective
noise introduced by digitization is not removed.
=0 tracks passed through the slow simulator with
varying levels of noise are used to study resolution and calculated
uncertainties. The amount of noise is quantified in terms of the
nominal electronics noise in the default simulator. Note that resolution
and uncertainty do not vanish at ``% noise''=0, because the effective
noise introduced by digitization is not removed.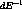 .
.

 =0 tracks, for all values of noise. Note the scale
change for resolution as the noise increases.
=0 tracks, for all values of noise. Note the scale
change for resolution as the noise increases.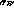 =0)
[
=0)
[ .
.

 and drift length L), and varying electronic noise.
The
RMS of the residual distribution was calculated as a function of
and drift length L), and varying electronic noise.
The
RMS of the residual distribution was calculated as a function of  ,
dE/dx, L,
,
dE/dx, L,  , and noise level.
No dependence of the padrow spatial resolution was seen as a function of
, and noise level.
No dependence of the padrow spatial resolution was seen as a function of
 or L, as expected since
or L, as expected since 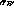 =0 (see above).
The dependence of the RMS on
=0 (see above).
The dependence of the RMS on  and signal size is shown in the
case of zero electronics noise in
Figure
and signal size is shown in the
case of zero electronics noise in
Figure 
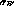 and
and 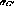 , which depend only on the chamber geometry and
gas properties [
, which depend only on the chamber geometry and
gas properties [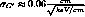 and for the
inner sector
and for the
inner sector 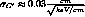 .
.
 will be determined after TSS is updated.
We note that the values for
will be determined after TSS is updated.
We note that the values for  may also change
if, for example, the energy loss gets calculated differently.
may also change
if, for example, the energy loss gets calculated differently.
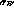 and
and 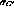 in hand,
and a hypothesis of
in hand,
and a hypothesis of  , can accurately estimate the uncertainty
of the hit position, as is shown in Figure
, can accurately estimate the uncertainty
of the hit position, as is shown in Figure 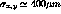 , whereas for those hits whose parent
tracks had
, whereas for those hits whose parent
tracks had 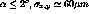 . It is this
small
. It is this
small  resolution that scales as signal:noise.
resolution that scales as signal:noise.

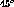 lines are drawn for
reference.
lines are drawn for
reference.