
In addition to being sorted based on velocity ratio, analyzer pulse height, and polar scattering angle, the data stored in the PAW ntuples need to be sorted by beam polarization state, (+) or (-), and azimuthal scattering angle, left or right. Once this is done the beam asymmetry

or,

as defined in equation ![]() , can be determined and the spin
observables calculated.
, can be determined and the spin
observables calculated.
Determining the location of the left and right sectors for the asymmetry
measurement, as discussed in section ![]() , is one of the places
in the
analysis where the use of the PAW ntuples is most beneficial. Typically
the full
, is one of the places
in the
analysis where the use of the PAW ntuples is most beneficial. Typically
the full 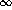 (azimuthal) range was split into four sectors -- left,
right, up,
and down -- which were hardwired in the replay and analysis. This works
fine in the investigation of discrete states but has problems when studying
a continuum. The neutron, after being produced in the target, will pass
through the series of precession magnets discussed in section
(azimuthal) range was split into four sectors -- left,
right, up,
and down -- which were hardwired in the replay and analysis. This works
fine in the investigation of discrete states but has problems when studying
a continuum. The neutron, after being produced in the target, will pass
through the series of precession magnets discussed in section ![]() .
The
neutron spin will be precessed to some direction, hopefully measurable in
the detector, which may or may not conform to the sectors chosen. Even
worse, the amount of precession is energy dependent. So the neutrons in
the tail will scatter with a different asymmetry in the detector than those
in the peak because they have been precessed by a different amount.
.
The
neutron spin will be precessed to some direction, hopefully measurable in
the detector, which may or may not conform to the sectors chosen. Even
worse, the amount of precession is energy dependent. So the neutrons in
the tail will scatter with a different asymmetry in the detector than those
in the peak because they have been precessed by a different amount.
Ordinarily, the corrections for the different precessions are made by weighting the results by a factor related to precession angle. However, this is not the most efficient method because the count difference between left and right scattered neutrons will be smaller and the overall statistical uncertainty will be larger.
The polarization vector of the neutron will be altered between the target to the detector as follows:
where 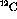 is the precession angle in the
is the precession angle in the
 plane from the dump magnet,
plane from the dump magnet,  is
the precession in the
is
the precession in the 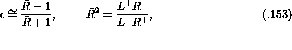 plane from the
combination of the permanent dipole and large, electromagnetic dipole,
and
plane from the
combination of the permanent dipole and large, electromagnetic dipole,
and  is
the precession in the
is
the precession in the  plane from the
neutron solenoid. The angles are calculated by the following formula
plane from the
neutron solenoid. The angles are calculated by the following formula

where 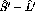 is the Landé g factor for the neutron,
is the Landé g factor for the neutron, 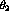 is
the nuclear magneton,
is
the nuclear magneton, 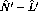 , and
, and 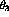 is the
integral of the magnetic field over the path of the neutron. The
is the
integral of the magnetic field over the path of the neutron. The
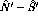 has been mapped out for each magnet.
See figure
has been mapped out for each magnet.
See figure ![]() for the position of these
magnets. Notice that the
for the position of these
magnets. Notice that the  solenoid was not used while measuring
neutrons in the
solenoid was not used while measuring
neutrons in the 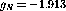 or
or 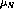 directions, and when
measuring
directions, and when
measuring 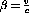 polarized neutrons the permanent dipole and
polarized neutrons the permanent dipole and
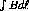 dipole were set so as to cancel each other out. Using the PAW
ntuples the optimum sectors (those centered at
dipole were set so as to cancel each other out. Using the PAW
ntuples the optimum sectors (those centered at 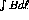 to the
nominal neutron polarization) are recalculated on an event-by-event basis,
subject to values of the neutron energy and the various magnetic fields.
to the
nominal neutron polarization) are recalculated on an event-by-event basis,
subject to values of the neutron energy and the various magnetic fields.
Obviously the sectors are based only on the expected polarization
components in the 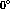 or
or 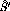 directions
since the
detector can only measure polarization components transverse to the neutron
flux direction.
Despite an effort to eliminate any longitudinal component to the neutron
polarization at the detector by adjusting the magnet settings and
optimizing
the precession angles, a small
directions
since the
detector can only measure polarization components transverse to the neutron
flux direction.
Despite an effort to eliminate any longitudinal component to the neutron
polarization at the detector by adjusting the magnet settings and
optimizing
the precession angles, a small 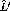 component will exist.
This fraction of the polarization which was rotated to the longitudinal
direction can be determined from the magnet characteristics and the small
correction made to the measured neutron polarization.
component will exist.
This fraction of the polarization which was rotated to the longitudinal
direction can be determined from the magnet characteristics and the small
correction made to the measured neutron polarization.