



Next: Experiment
Up: INTRODUCTION
Previous: Prologue
Quantum Chromodynamics (QCD) is generally considered to be the underlying
theory of nuclear physics with the gluon as the carrier of the
strong force. However, because of the non-perturbative nature of QCD at
low and intermediate energies, direct calculations of the nucleon-nucleon
(nn) interaction and its implications for nuclei are not yet possible.
What is known about QCD at low energies is usually deduced from the
symmetries
of that theory, such as the 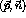 symmetry.
It has been shown [NaW79] that when the chiral
symmetry
of QCD with two massless quarks is spontaneously broken, this
results in a massless Goldstone boson associated with the
conserved axial vector current. Because of the small, but non-zero,
masses of the u and d quarks the axial vector current is only partially
conserved, and the Goldstone boson resulting from the
breaking of chiral
symmetry will be a massive, but light, pseudoscalar boson that is
the pion. It has also been shown that [WeW81] by employing PCAC
(partially conserved axial current) in the case of pseudoscalar coupling of
a
symmetry.
It has been shown [NaW79] that when the chiral
symmetry
of QCD with two massless quarks is spontaneously broken, this
results in a massless Goldstone boson associated with the
conserved axial vector current. Because of the small, but non-zero,
masses of the u and d quarks the axial vector current is only partially
conserved, and the Goldstone boson resulting from the
breaking of chiral
symmetry will be a massive, but light, pseudoscalar boson that is
the pion. It has also been shown that [WeW81] by employing PCAC
(partially conserved axial current) in the case of pseudoscalar coupling of
a 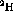 -pair to the pion at the hadron surface, the form and
coupling strength of the
-pair to the pion at the hadron surface, the form and
coupling strength of the 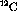 vertex is consistent with the
phenomenological OPEP (one pion exchange potential).
vertex is consistent with the
phenomenological OPEP (one pion exchange potential).
Given the results of those studies [WeW81] [NaW79] of the
effects of chiral symmetry it
seems a reasonable extension of QCD, and a more tractable problem, to
treat mesons, and in particular pions, as the carriers of the nuclear
force. Therefore, the nn interaction,
specifically at intermediate and long ranges, is primarily
described through meson exchange. Table  gives a list
of the lightest mesons (and their properties) which are used in meson
exchange models.
gives a list
of the lightest mesons (and their properties) which are used in meson
exchange models.
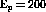
Table: Light unflavored mesons [PDH96].
If mesons are truly the carriers of the nuclear force, modern
calculations based on a model of meson exchange predict that the pion field
in the nucleus is enhanced by the collective action of
the many nucleons in the nucleus. Details of the model are given in
chapter  .
This enhanced field should have an effect on many experimentally
observable
properties of the nucleus, particularly those induced by external pion
fields [BFS93].
.
This enhanced field should have an effect on many experimentally
observable
properties of the nucleus, particularly those induced by external pion
fields [BFS93].
During the past decade a variety of experiments have returned no evidence
that this enhancement actually exists. For instance, a measurement of
muon pair production in p-nucleus scattering at 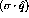 GeV done
at Fermi
National Accelerator Lab (FNAL) showed no enhancement in large nuclei
compared to
GeV done
at Fermi
National Accelerator Lab (FNAL) showed no enhancement in large nuclei
compared to 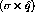 for the target-quark momentum fraction range
for the target-quark momentum fraction range
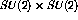 [Ald90]. Since the muon pairs are primarily
produced via
[Ald90]. Since the muon pairs are primarily
produced via
 (the Drell-Yan effect) this lack of
enhancement indicates a lack of anti-quarks in the nucleus which, in turn,
indicates no enhancement in the pion field [Ald90].
(the Drell-Yan effect) this lack of
enhancement indicates a lack of anti-quarks in the nucleus which, in turn,
indicates no enhancement in the pion field [Ald90].
The collective enhancement of the nuclear pion field should also have an
effect on the scattering of nucleons from the nucleus. In particular an
investigation of the spin-isospin dependent part of the nn interaction
should reveal a change in the pion field with respect to the free case.
Because the pions' interaction differs on whether the nucleon spin is
parallel or normal to the direction of momentum transfer (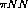 ) a
measurement of the polarization transfer in a nucleon-nucleus collision
should reveal information about the pion field.
) a
measurement of the polarization transfer in a nucleon-nucleus collision
should reveal information about the pion field.
In 1982 Alberico, Ericson, and Molinari [AEM82] predicted that
there should be a
noticeable difference between spin-longitudinal 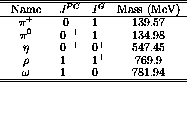 isospin response and the spin-transverse
isospin response and the spin-transverse 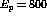 isospin
response of the nucleus due to this enhancement in the pion field for
momentum transfers between
isospin
response of the nucleus due to this enhancement in the pion field for
momentum transfers between
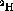 and
and 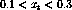 . The
specifics of the prediction will be discussed in chapter
. The
specifics of the prediction will be discussed in chapter  .
.




Next: Experiment
Up: INTRODUCTION
Previous: Prologue
Michael A. Lisa
Tue Apr 1 08:52:10 EST 1997
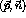 symmetry.
It has been shown [NaW79] that when the chiral
symmetry
of QCD with two massless quarks is spontaneously broken, this
results in a massless Goldstone boson associated with the
conserved axial vector current. Because of the small, but non-zero,
masses of the u and d quarks the axial vector current is only partially
conserved, and the Goldstone boson resulting from the
breaking of chiral
symmetry will be a massive, but light, pseudoscalar boson that is
the pion. It has also been shown that [WeW81] by employing PCAC
(partially conserved axial current) in the case of pseudoscalar coupling of
a
symmetry.
It has been shown [NaW79] that when the chiral
symmetry
of QCD with two massless quarks is spontaneously broken, this
results in a massless Goldstone boson associated with the
conserved axial vector current. Because of the small, but non-zero,
masses of the u and d quarks the axial vector current is only partially
conserved, and the Goldstone boson resulting from the
breaking of chiral
symmetry will be a massive, but light, pseudoscalar boson that is
the pion. It has also been shown that [WeW81] by employing PCAC
(partially conserved axial current) in the case of pseudoscalar coupling of
a 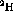 -pair to the pion at the hadron surface, the form and
coupling strength of the
-pair to the pion at the hadron surface, the form and
coupling strength of the 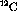 vertex is consistent with the
phenomenological OPEP (one pion exchange potential).
vertex is consistent with the
phenomenological OPEP (one pion exchange potential).
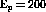
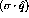 GeV done
at Fermi
National Accelerator Lab (FNAL) showed no enhancement in large nuclei
compared to
GeV done
at Fermi
National Accelerator Lab (FNAL) showed no enhancement in large nuclei
compared to 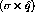 for the target-quark momentum fraction range
for the target-quark momentum fraction range
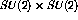 [
[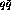 (the Drell-Yan effect) this lack of
enhancement indicates a lack of anti-quarks in the nucleus which, in turn,
indicates no enhancement in the pion field [
(the Drell-Yan effect) this lack of
enhancement indicates a lack of anti-quarks in the nucleus which, in turn,
indicates no enhancement in the pion field [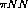 ) a
measurement of the polarization transfer in a nucleon-nucleus collision
should reveal information about the pion field.
) a
measurement of the polarization transfer in a nucleon-nucleus collision
should reveal information about the pion field.
 isospin response and the spin-transverse
isospin response and the spin-transverse 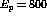 isospin
response of the nucleus due to this enhancement in the pion field for
momentum transfers between
isospin
response of the nucleus due to this enhancement in the pion field for
momentum transfers between
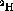 and
and 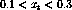 . The
specifics of the prediction will be discussed in chapter
. The
specifics of the prediction will be discussed in chapter