



Next: EXPERIMENTAL PROCEDURE
Up: FORMALISM
Previous: Response Functions
In order to factor out the expression for total nA cross section into
the product of several independent terms such as
the nn cross section, response function, and other corrections (eqn.
 ) the assumption must be made that the nn amplitudes depend
only on the incident energy and the momentum transfer, q. However, in
general, the stuck nucleon will have its own momentum,
) the assumption must be made that the nn amplitudes depend
only on the incident energy and the momentum transfer, q. However, in
general, the stuck nucleon will have its own momentum, 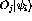 , due to
Fermi motion which enters the problem and can break down that simple
factorization. Instead of integrating over the struck nucleon's Fermi
momentum the process becomes much simpler if the nn amplitudes can be
factored out by evaluating them in some ``optimal'' frame where the struck
nucleon has a constant value,
, due to
Fermi motion which enters the problem and can break down that simple
factorization. Instead of integrating over the struck nucleon's Fermi
momentum the process becomes much simpler if the nn amplitudes can be
factored out by evaluating them in some ``optimal'' frame where the struck
nucleon has a constant value, 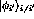 . This procedure has been
discussed in [Gur86], [Smi88], and in detail in [IcK92].
For inelastic scattering, in the non-relativistic case, the optimal
momentum was worked out to be [Gur86]
. This procedure has been
discussed in [Gur86], [Smi88], and in detail in [IcK92].
For inelastic scattering, in the non-relativistic case, the optimal
momentum was worked out to be [Gur86]
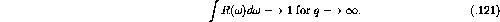
Notice, the optimal momentum will be zero for free scattering where
 .
.
The scattering matrix in the optimal frame, 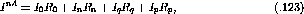 , is related to the nn
scattering matrix, M (eqn.
, is related to the nn
scattering matrix, M (eqn.  ) by [Che93]
) by [Che93]

where 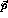 is the incident proton energy,
is the incident proton energy,  is the Möller
(kinematic) factor, and
is the Möller
(kinematic) factor, and  is the matrix which performs the frame
rotation as defined in [IcK92]. The new scattering matrix can be
written as
is the matrix which performs the frame
rotation as defined in [IcK92]. The new scattering matrix can be
written as

with the spin-dependent pieces being defined

where the superscript 0 indicates the incoming proton and the superscript
i denotes a sum over A nucleons. The amplitudes (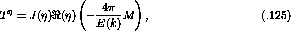 ,
, 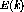 ,
etc.) are related to those in equation
,
etc.) are related to those in equation  by equation
by equation  .
From the equations above it can be seen that
.
From the equations above it can be seen that 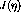 (
(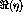 ) does
not excite the purely longitudinal(transverse) mode in the optimal frame.
Therefore,
) does
not excite the purely longitudinal(transverse) mode in the optimal frame.
Therefore, 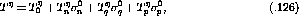 and
and  are no longer related directly to the
spin-longitudinal and spin-transverse nuclear response functions. Instead,
the nA center-of-mass partial cross sections,
are no longer related directly to the
spin-longitudinal and spin-transverse nuclear response functions. Instead,
the nA center-of-mass partial cross sections, 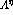 's, given by
's, given by

will be

where 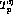 is a kinematic factor defined in [Che93] and
is a kinematic factor defined in [Che93] and 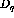 is the distortion factor.
is the distortion factor.
Obviously the choice of the optimal reference frame somewhat distorts the
simple relationship between the center-of-mass spin observables, 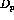 's,
and the nuclear response functions. However, it is the only way to deal
with amplitudes consistently over a range of energy transfers, such as in
the quasifree region, without violating energy conservation in each nn
(nucleon-nucleon) interaction.
's,
and the nuclear response functions. However, it is the only way to deal
with amplitudes consistently over a range of energy transfers, such as in
the quasifree region, without violating energy conservation in each nn
(nucleon-nucleon) interaction.




Next: EXPERIMENTAL PROCEDURE
Up: FORMALISM
Previous: Response Functions
Michael A. Lisa
Tue Apr 1 08:52:10 EST 1997
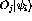 , due to
Fermi motion which enters the problem and can break down that simple
factorization. Instead of integrating over the struck nucleon's Fermi
momentum the process becomes much simpler if the nn amplitudes can be
factored out by evaluating them in some ``optimal'' frame where the struck
nucleon has a constant value,
, due to
Fermi motion which enters the problem and can break down that simple
factorization. Instead of integrating over the struck nucleon's Fermi
momentum the process becomes much simpler if the nn amplitudes can be
factored out by evaluating them in some ``optimal'' frame where the struck
nucleon has a constant value, 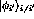 . This procedure has been
discussed in [Gur86], [Smi88], and in detail in [IcK92].
For inelastic scattering, in the non-relativistic case, the optimal
momentum was worked out to be [Gur86]
. This procedure has been
discussed in [Gur86], [Smi88], and in detail in [IcK92].
For inelastic scattering, in the non-relativistic case, the optimal
momentum was worked out to be [Gur86]
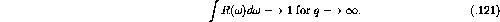
 .
.
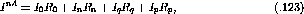 , is related to the nn
scattering matrix, M (eqn.
, is related to the nn
scattering matrix, M (eqn. 
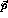 is the incident proton energy,
is the incident proton energy,  is the Möller
(kinematic) factor, and
is the Möller
(kinematic) factor, and  is the matrix which performs the frame
rotation as defined in [
is the matrix which performs the frame
rotation as defined in [

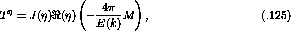 ,
, 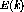 ,
etc.) are related to those in equation
,
etc.) are related to those in equation 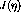 (
(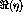 ) does
not excite the purely longitudinal(transverse) mode in the optimal frame.
Therefore,
) does
not excite the purely longitudinal(transverse) mode in the optimal frame.
Therefore, 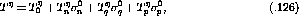 and
and  are no longer related directly to the
spin-longitudinal and spin-transverse nuclear response functions. Instead,
the nA center-of-mass partial cross sections,
are no longer related directly to the
spin-longitudinal and spin-transverse nuclear response functions. Instead,
the nA center-of-mass partial cross sections, 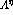 's, given by
's, given by


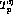 is a kinematic factor defined in [
is a kinematic factor defined in [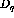 is the distortion factor.
is the distortion factor.
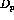 's,
and the nuclear response functions. However, it is the only way to deal
with amplitudes consistently over a range of energy transfers, such as in
the quasifree region, without violating energy conservation in each nn
(nucleon-nucleon) interaction.
's,
and the nuclear response functions. However, it is the only way to deal
with amplitudes consistently over a range of energy transfers, such as in
the quasifree region, without violating energy conservation in each nn
(nucleon-nucleon) interaction.