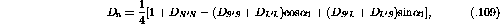
To this point in the formalism only nucleon-nucleon (nn) scattering has been considered. In order to relate this to the nucleon-nucleus (nA) scattering of the experiment it is necessary to introduce the idea of nuclear response functions. The cross section for the nA collision can be expressed in terms of the nn cross section [KMT59] [BeS82]:
where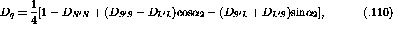 
is the free nn cross section, 
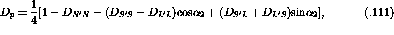is the effective number of nucleons, which for 
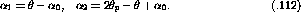reactions would be
neutrons, that can participate in the reaction. This is also sometimes
called the distortion factor [Che93]. The effective number of
nucleons will, in general, be less than the full number of nucleons in the
nucleus because the projectile nucleon will be strongly attenuated as it
travels through the bulk of the nucleus--exactly how much is a function of
energy--and therefore a portion of the possible target nucleons will be
shadowed.
The Response Functions,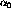 
, to a given projectile scattering
operator,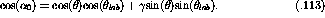 
,
are defined as [IcK92] [Bro95]:
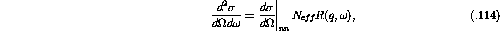
where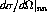 
is the nuclear wavefunction. The operators, 
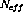, can be
defined as corresponding to the spin operators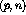 
, where
j = 0,n,p,q:
The operators,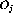 
, are then defined as
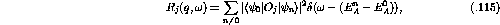
where sum is over the number of neutrons, N, and the normalization means
that the response is given as the response per neutron. In the limit of no
Pauli Blocking (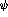
orthogonal to all
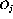) [Che93] [BeS82]
Just as the total cross section for nn scattering can be defined as the sum
of the partial cross sections defined in equations 
to
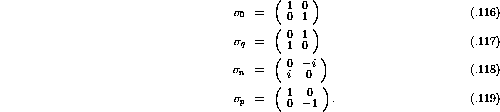
one can use the response functions to define the nA scattering cross
section. As can be inferred from equation the nA cross section
is given by
where the 
's are still the partial nn cross sections.
