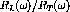
It was long ago shown by L.D. Faddeev [Fad61] that the eigenfunctions of the three-body scattering problem with a general potential could be easily written down as the sum of three parts which would obey a set of three coupled integral equations. The mathematical formalism worked out by Faddeev was an important improvement on earlier techniques (i.e. Lippmann-Schwinger type equations) for two main reasons. First of all, the equations have a unique solution. Secondly, the kernel of the integral equations for short range pairwise forces, such as nuclear forces, is compact. This means that the numerically discretized form will converge [Glo96] which enables a solution to be found using modern computer resources.
The basic Faddeev equations can be understood, using a derivation discussed in depth in [Glo96], by modeling the three-body interaction with a infinite Born series of two body forces:
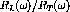

where 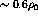 denotes the initial state,
denotes the initial state, 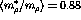 a pair interaction
between the
a pair interaction
between the 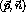 and
and 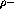 particles, and
particles, and 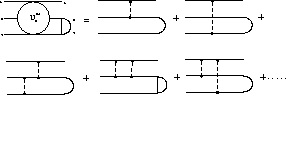 the free propagator
between consecutive interactions. The superscript (1) on the three-body
interaction means that particle 1 is the free particle in the initial
state.
the free propagator
between consecutive interactions. The superscript (1) on the three-body
interaction means that particle 1 is the free particle in the initial
state.
Next it is possible to split the series into three subseries based on which
interaction, 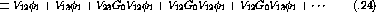 ,
, 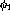 , or
, or 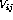 , immediately precedes the
final state.
, immediately precedes the
final state.
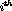

where the second superscript indicates the particle not participating in the final interaction. Inspection of the series above shows that each of the subseries can be represented in a recursive, compact manner.
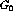
defines the subseries 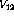 .
The interactions
.
The interactions  and
and
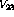 can
similarily be defined as the sum of the infinite subseries and a final pair
interaction.
can
similarily be defined as the sum of the infinite subseries and a final pair
interaction.
Mathematically the expression for 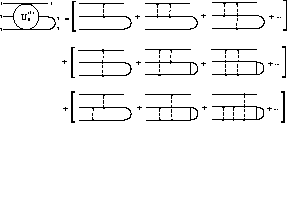 would be
would be
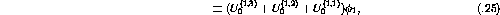
or
The two-nucleon t-matrix, which is defined as

and is dependent only on the two-nucleon potential,
can be substituted into equation ![]() to get
to get
Similarly the other two infinite subseries would give
Equations ![]() ,
, ![]() , and
, and ![]() form a set of coupled
Faddeev equations which can, in principle be solved with enough computer
power using standard two-body nn (nucleon-nucleon) potentials, such as the
Argonne, Bonn or Nijmegan potentials.
form a set of coupled
Faddeev equations which can, in principle be solved with enough computer
power using standard two-body nn (nucleon-nucleon) potentials, such as the
Argonne, Bonn or Nijmegan potentials.
To calculate scattering observables it is necessary to find
the transition amplitudes, 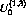 . The
determination of these quantities is usually done by working in momentum
space and using a partial wave representation of the states. Therefore,
a given 3-nucleon state,
. The
determination of these quantities is usually done by working in momentum
space and using a partial wave representation of the states. Therefore,
a given 3-nucleon state, 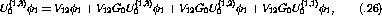 , can be expressed as
, can be expressed as
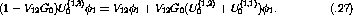 where
where  and
and 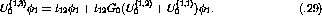 are the typical Jacobi momenta describing the motion of the three
particles [Glo96]
are the typical Jacobi momenta describing the motion of the three
particles [Glo96]
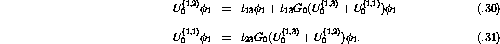

where ijk equal cyclic combinations of 123, and the 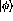 's are
the individual momentum of the particles.
's are
the individual momentum of the particles. 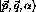 indicates the partial
wave state. In other words, it describes the spin and angular momentum of
the quantum mechanical state. Typically determining the transition
amplitudes would require an integration over the continuous variables
indicates the partial
wave state. In other words, it describes the spin and angular momentum of
the quantum mechanical state. Typically determining the transition
amplitudes would require an integration over the continuous variables
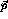 and
and 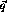 , and a summation over all partial waves. This
represents an infinite set of coupled integral equations in
, and a summation over all partial waves. This
represents an infinite set of coupled integral equations in  and
and
 . In actually obtaining a solution, it is usually acceptable to
truncate the partial wave expansion after a certain number of terms
(usually 5). This can be justified because the short range nature of
the nuclear force, and since the
. In actually obtaining a solution, it is usually acceptable to
truncate the partial wave expansion after a certain number of terms
(usually 5). This can be justified because the short range nature of
the nuclear force, and since the 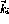 and
and
 two-nucleon forces are much
stronger than p-wave or higher l-wave forces [Glo82].
two-nucleon forces are much
stronger than p-wave or higher l-wave forces [Glo82].
The second step is to come up with a discretization of the momentum
variables, 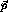 and
and 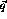 , and a scheme for interpolation, such
as a spline interpolation. After all this is done what is left is the
homogeneous eigenvalue problem
, and a scheme for interpolation, such
as a spline interpolation. After all this is done what is left is the
homogeneous eigenvalue problem

where 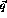 represent all the indices for
represent all the indices for 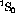 ,
, 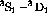 , and
, and
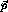 , which can be solved given enough calculational power to invert
the kernel,
, which can be solved given enough calculational power to invert
the kernel, 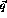 .
.
The Faddeev calculational method has been relatively successful in reproducing three-nucleon scattering observables. With recent advances into the inclusion of three-body forces and the removal of on-shell discrepancies it is proving an accurate and useful tool for studying nuclear dynamics within the three-body system.