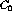In order to correct the Landau-Migdal interaction to account for the finite
range of the NN interaction the contribution due to meson exchange can be
included explicitly. This correction would seem to be especially important
in the spin-isospin channel because of the contribution of the lightest
meson, the pion. If the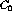 
meson is also included as the other
isovector meson which could contribute the p-h force will take the form
[Ost92]
where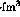 
is a phenomenological constant related to the
Landau-Migdal parameter 
. The 
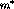and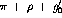 
exchange terms
do not describe well the short range behavior of the interaction so it is
necessary to keep the contact term, which accounts for heavy meson and QCD
effects. This is the so-called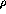 
model for the
isovector p-h interaction.
In momentum space the particle-hole potential for the
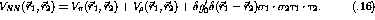model is given by [ETB85]
where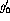 
is the meson-nucleon coupling constant 
,
is the energy loss, q is the momentum transfer,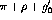 
is the
meson mass, and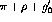 
is the monopole vertex form factor which takes
the form [OTW82]
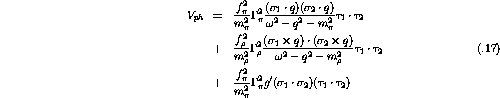
The cut-off mass, 
, is inversely related to the range of the
meson-nucleon vertex and must be determined phenomenologically from the
short range behavior. It is obvious from equation 
that,
because of its pseudoscalar nature, the pion is primarily responsible
for the spin-longitudinal 
response while the
part dominates the spin-transverse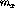 
response.
Through use of the identity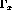 
we can separate equation into
the spin-longitudinal and spin-transverse parts [McC92]:
where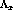 
.
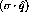
Figure: The momentum transfer dependence of the residual
particle-hole interaction due to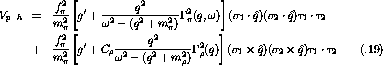 
and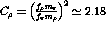 
meson exchange. The
dashed line shows the 
dependence and the
dotted line shows the 
dependence of the interaction. [Pro91]
The separate spin-longitudinal and spin-transverse parts of the
particle-hole force are plotted in figure with 
,
GeV,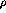 
GeV, and 
.
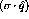Both components of the force are repulsive at short range, but, due to the
small pion mass, the spin-longitudinal part becomes attractive at around 1
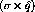while the transverse part remains repulsive until 
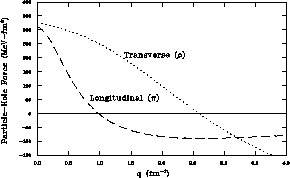. Therefore, using
the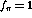 
model for the residual particle-hole
interaction in their RPA calculations, Alberico et al. [AEM82]
predicted the transverse response would be quenched and hardened while the
longitudinal response is softened and enhanced, particularly between
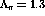to 
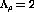. This means that the ratio of the
longitudinal to the transverse responses should be larger at small energy
loss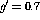 
in nA collisions than in nn collisions, as shown in figure
.
