Describing two particles
We have seen that the state of one electron can be described by giving its wavefunction; i.e., the shape of its wave. Suppose we also have a second particle, a proton. How should we describe the state of the full system consisting of an electron and a proton?
A first attempt
At first the answer appears to be straightforward: we choose a waveform for the electron, and a waveform for the proton.
While such a description is not wrong, it gives only a small subset of all the possible states that these two particles can have.
To see this, let us start with simple wavefunctions for the electron and proton. The electron wavefunctions is made of two equal and well-separated bumps, so the electron can be on the left or the right with \( 50\%\) probability for each possibility. The proton wavefunction is also taken to have two similar bumps.
Our full set of probabilities reads as follows:
- Electron on left, proton on left: probability \( \frac{1}{2} \times \frac {1}{2} = \frac{1}{4} \)
- Electron on left, proton on right: probability \( \frac{1}{2} \times \frac {1}{2} = \frac{1}{4} \)
- Electron on right, proton on left: probability \( \frac{1}{2} \times \frac {1}{2} = \frac{1}{4} \)
- Electron on right, proton on right: probability \( \frac{1}{2} \times \frac {1}{2} = \frac{1}{4} \)
Requiring a different probability set
Now suppose we demand the following probabilities:
- Electron on left, proton on left: probability \( \frac{1}{2} \)
- Electron on right, proton on right: probability \( \frac{1}{2} \)
Why should we be interested in such a set of probabilities? Suppose the electron and proton were bound together into an atom. Then the electron would be always near the proton. We could ask that the whole atom be on the left or the right with equal probabilities. But this would still give only two possibilities: both electron and proton on the left, or both electron and proton on the right.
But we do not get probabilities describing such an atom if we draw separate wavefunctions for the electron and the proton; we will instead get all the four possibilities listed in section 2 above. So we need a more general understanding of wavefunctions.
A function of two variables
Recall that the waveform of an electron described the amplitude of the electron wave at any position \( x \); squaring this amplitude gave the probability for the electron to be at \( x \).
With two particles - the electron and the proton - we proceed as follows:
- We draw an axis labelled \( x_1\) to describe the position of the electron
- We draw another axis labelled \( x_2\) to describe the position of the proton.
- We thus get a 2-dimensional plane. The point \( (x_1,x_2) \) of this plane corresponds to the electron having the position \( x_1\) and the proton having the position \( x_2 \).
- When we had only one particle present (the electron), we described the system by giving an amplitude for each position \( x \) that the electron could be at. With both the electron and the proton present, we need to give an amplitude for each possible set of numbers \( ( x_1, x_2 ) \) describing the positions of our two particles. This amplitude function describes a wave over our 2-dimensional plane.
- Squaring the amplitude at a point \( (x_1, x_2) \) gives the probability that the electron is at \( x_1\) and the proton is at \( x_2 \).
Constructing examples
In section 2 we had taken separate wavefunctions for the electron and proton; each of these had a \( 50 \% \) probability to be on the left or the right. On our 2-dimensional space, the wavefunction is depicted in fig. 1. There are 4 bumps. In the bottom left corner we have a bump where \( x_1\) and \( x_2 \) are both negative; this corresponds to the electron on the left and the proton on the left. A similar interpretation holds for the other three bumps.
Now consider the atom described in section 3; this atom had a \( 50\% \) probability of being on the left or right. The corresponding wavefunction is given in fig 2. There is a bump in the bottom left corner where \( x_1\) and \( x_2 \) are both negative; this corresponds to the electron on the left and the proton on the left, so the whole atom is on the left. Similarly there is a bump in the top right corner where \( x_1\) and \( x_2 \) are both positive; this corresponds to the electron on the right and the proton on the right, so the whole atom is on the right.
So we see that by considering waves over the 2-dimensional \( x_1-x_2 \) plane, we have been able to describe both the situation of sec.2 and the situation of sec. 3. By contrast, in fig.1 we had taken two different waves, but each was only defined over a 1-dimensional line \( x\). This 1-dimensional description does not allow for all possible situations that we wish to describe.
Summary
We see that if we have two particles, then the wavefunction should be written as a function of two variables \( x_1\) and \( x_2 \). There is a vast set of such functions, so that we can describe many more possibilities than we could if we considered separate wavefunctions for the two particles.
Our next question is: how do we characterize the extra possibilities that are allowed when we use a function of two variables?
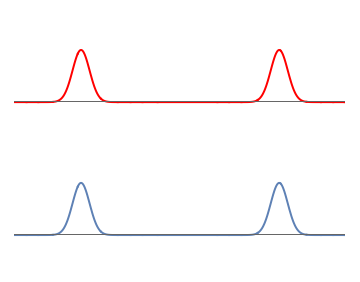
1: Separate waves for the proton (red) and the electron (blue). Each wave consists of two well-separated bumps.
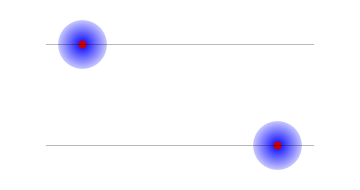
2: An atom on the left and an atom on the right; in each case the proton and the electron are on the same side.
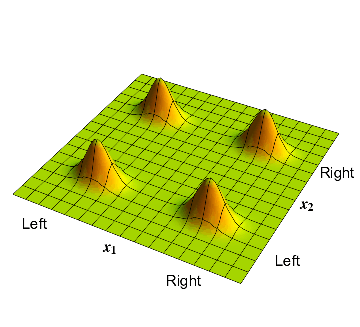
3: The waveform over the 2-dimensional \( x_1-x_2\) plane, describing an electron and a proton which have independent probabilities to be on the left and on the right.
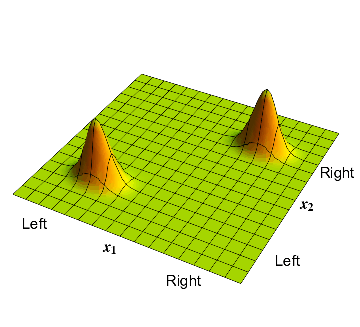
4: The waveform which has the electron and proton on the same side; but the overall position of the pair can be on the left or on the right.