Analyzing the experiment
We have considered a waveform which had two well separated bumps. The waveform had the strength which describes one electron, and an electron cannot split in half. So we were forced to a strange conclusion: the location of the electron can only be described in terms of probabilities; there is a \( 50\%\) probability that it is located at the left bump and a \( 50\%\) probability that it is located at the right bump.
This conclusion is a bizzare one. To be sure that it is correct, we ask how an experiment would be set up to check that we indeed get this randomness of outcomes. There are two natural questions:
- Can we really create a waveform with the shape of two well-separated bumps?
- How do we check that there is indeed a whole electron near the left or right bumps?
Creating the waveform
Consider a hill as shown in fig.1. Suppose we put a lump of water on the top of this hill. The water will slosh down; half to the left and half to the right. After a time, we will have two well-separated waves.
We can do the same thing with an electron wave. Take a negatively charged ion; the ion is heavy and we assume that it does not move. Now bring this ion near an electron. Since two negatively charged objects repel, the electron will have to move away from the ion.
The electron is described by a wave, and this wave behaves much like the water wave above. Half the wave will move to the left, and half to the right. After some time, we will indeed be left with an electron wave in the shape of two well-separated bumps.
So we see that it is indeed possible to create the kind of waveform that led to our puzzling experiment.
Detecting the electron
We wish to construct a detector that will tell us if an electron is present at a given location; further, it should tell us if this is a full electron or half an electron.
Imagine a thin glass tube, with both ends closed, oriented in the vertical direction. We place an muon in this tube. A muon is a particle with the same negative charge as the electron, but with a mass that is about \( 200 \) times more. This device will be called our 'detector'.
We place this tube at the location where we wish to detect the presence of an electron. The following will happen:
- If there is no electron near the detector, the muon will stay at the bottom of the tube.
- If there is a whole electron near the detector, then the muon will be repelled, and rise up to the top of the tube.
- If there is a 'half' electron near the detector, then the muon will feel a smaller repulsive force, and therefore rise only halfway up the tube.
Thus this detector can tell us if at some location we have no electron, half an electron, or one full electron.
Performing the experiment
- Construct an electron wave with the shape of two well-separated bumps; one on the left (\(L\)) and one on the right (\(R\)). Let us assume that we have done this by the method described above; i.e, by using an ion to repel the electron away from the middle.
- Place one detector near the left bump and one near the right bump.
- A possible outcome is as follows. The left detector shows a full electron, and the right shows no electron.
- We now redo the experiment again from the start; i.e., we construct the waveform by starting with an ion which repels the electron wave to the desired shape. We again place a detector near each bump. This time we might find an electron near the right bump, and no electron near the left bump.
- We carry out this process many more times. Each time we construct the two-bump waveform in exactly the same way, and look for the electron with out detectors. We never find an electron on both sides. We also never find a half electron on either side. What we find is a single whole electron, but its location could be left or right, with this choice being completely random. Thus our sequence of identical experiments may furnish an outcome like \[ L, ~R, ~R, ~L, ~L, ~R, ~L, \dots \] where the only thing we can say about the sequence is that on average we get \(L\) \(50\%\) of the time and \(R\) \(50\%\) of the time.
This experiment illustrates a behavior which encodes the essence of quantum mechanics.
Checking for flaws
One might think that this random behavior is arising because we tried to split the wavefunction \( 50 - 50 \) into two halves. Since an experiment can never be fully accurate, it might be that the split is actually \( 51-49\) in some instances of the experiment, and \(49-51\) in others. Could it be that the first set gives the \( L \) detections and the second set the \( R \) detections?
But this worry is easily dispelled. We can look at wavefunctions where the strength of the left bump is \( 2/3\) and that of the right bump is \( 1/3\). So the wave is always stronger on the left. But when we repeat the experiment many times, we find that we detect the electron on the left \( 2/3\) of the time, and on the right \( 1/3\) of the time.
To summarize, we have now seen explicitly how to set up an experiment which has two possible outcomes, and where it is not possible to predict in advance which one possibility will happen.
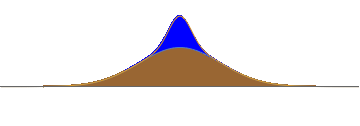
1: A lump of water is kept on a hill. The natural evolution of the wave divides it into two parts.
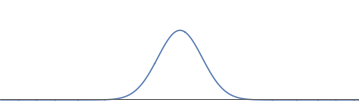
2(a): We start with an electron wave with a single bump; this describes an electron localized near one place.
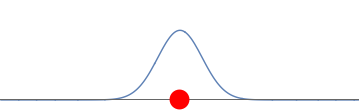
2(b): A negatively charged ion is placed in the middle of the waveform. The ion repels the electron creating two well-separated bumps.
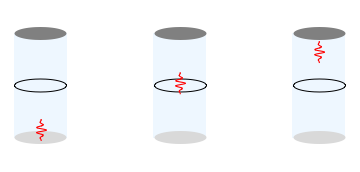
3: A detector for the electron. If no electron is present, the muon stays in the 'down' position. If half an electron is present, the muon will rise halfway up the cylinder. If a full electron is present, the muon will rise to the top of the cylinder.

4(a): One iteration of the experiment. Start with a wavefunction with two bumps.

4(b): Detectors are placed near the left and right bumps.

4(c): The muon in the detector rises to the top at the left bump, signaling a full electron on the left. The muon in the right detector does not rise at all, signaling no electron on the right.

5(a): Another iteration of the experiment. Make the same wavefunction in exactly the same way as before.

5(b): Detectors are placed near the left and right bumps.

5(c): Though we repeat the experiment exactly as before, this time we detect the electron on the right.
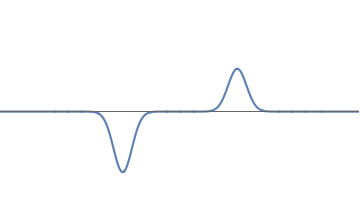
6(a): A asymmetric wave, with strengths \( 2/3\) and \( 1/3 \) in the left and right bumps respectively.

6(b): Detecting the electron for this waveform. On different tries, we get different results, with probability \( 2/3 \) for detection on the left and \( 1/3\) for detection on the right.