The ingredients for the puzzle
To explain our main puzzle, let us collect here the rules we have learnt for quantum theory:
- Everything is a wave; thus an electron is a wave, just like radio waves are waves.
- All waves have a curious property: their strength comes in discrete units. We can call this discreteness the 'particle like' behavior of the wave. Thus we cannot have half a photon, just like we cannot have half an electron.
Putting these two observations together leads to a very deep puzzle.
The puzzle
Now we ask: what does this wave describe? Let us consider different possibilities:
- We have two electrons; one at the left bump and one at the right bump. But this does not make sense. We have kept the strength of the wave the same, so all through the deformation from Fig 1(a) to Fig 1(c), the number of electrons should have remained one.
- We have half an electron at the left bump and half an electron at the right bump. But this cannot be correct either. Suppose we look near the left bump, which is on Earth. If this described half an electron, then we should see a particle with half the mass and half the charge of an electron, But we have never seen such a thing.
An important conclusion
We are thus forced to the following rather bizzare conclusion:
The wave of fig.1(c) describes one electron; further, this electron does not split into two halves. But there is a 50% probability that the whole electron is located at the left bump (i..e on Earth) and a 50% probability that the whole electron is located at the right bump (i.e. on Mars).Does God play dice?
The above conclusion is correct but very puzzling, and summarizes the entire mystique of quantum mechanics.
The conclusion is puzzling because in all earlier theories of physics, everything had been definite; we know whether an electron is on Earth or on Mars. But in quantum theory, for waveform of the kind in fig.1(c), all we have is a probability for the electron to be at different positions; we cannot say with definiteness where the electron is.
This situation was so uncomfortable to Einstein that at first he refused to accept it, saying "God does not play dice"; i.e., the description of nature must be definite and not in terms of probabilities.
The way we understand things today
Once quantum theory was better understood, the worries of the kind raised by Einstein disappeared. It turns out that two things are true:
- The above description in terms of probabilities is correct.
- Underlying these probabilities is an evolution of waves that is definite. The notion of probabilities arises when we use the waveform to predict the result of measurements.
In the rest of this chapter we will study the notion of probabilities in more detail; i.e., we focus on (1). In the next chapter we will understand the measurement process, thus clarifying (2).
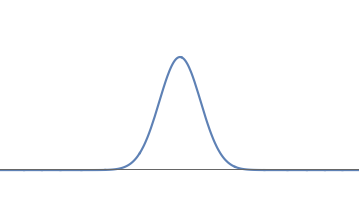
1(a): A simple waveform for the electron, consisting of one 'bump'.
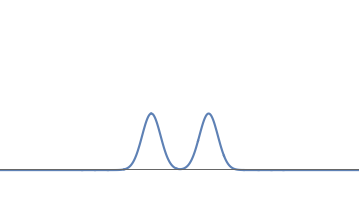
1(b): We can deform this waveform to get another one, consisting of two bumps.
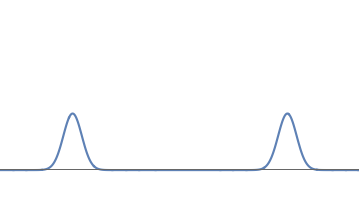
1(c): We can deform the waveform further, getting two well-separated bumps.