Similarities between particles and waves
We have talked about particles and waves, and the fact that in quantum mechanics everything is a wave. But what is the important property that waves have but particles do not?
Before we come to this important difference, let us note that there are many similarities between particles and waves:
- Particles can move, with this motion described by a direction and speed. Waves can also move, and again this motion has a direction and speed.
- Particles carry energy; waves also carry energy.
- Particles can carry momentum: a moving particle can collide with and 'push' another object. Waves can also carry momentum: e.g. ocean waves can hit and topple a ship.
The important difference between particles and waves
The relevant property of waves is that waves can cancel. Suppose two water waves are coming to the same place. Let one have a crest at this place, and the other a trough. Then the waves will cancel at this place; i.e., that the water will neither go up nor down.
The waves in quantum mechanics have a similar cancellation property. This is in sharp contrast to what would happen with particles: if two particles reach a given place then we will have two particles there; they cannot cancel out to leave zero particles.
Let us now see the cancellation of waves more explicitly.- Fig.1a shows a wave traveling to the right. The blue color corresponds to the places where the wave height is positive; thus the darkest blue points line on the wave crests. The yellow color corresponds to the places where the wave height is negative; thus the darkest yellow points line on the wave troughs. White describes the points where the wave height is zero; i.e., halfway between the crest and the trough.
- Fig.1b shows a similar wave traveling in the up direction.
- Fig.1c shows the situation where we have both waves present together. We have arranged things so that the crest of the right-moving wave falls on the troughs to the up-moving wave. In the central region marked with a circle, the waves cancel. Thus this central location remains white at all times.
The cancellation of electron waves
Since electrons are waves, the cancellation of Fig.1c will happen for electron waves as well. But what will this cancellation mean?
The wave going to the right describes an electron beam headed to the right. The wave going up describes a beam of electrons headed up. Suppose we have arranged these beams to have the wave structure of Fig 1c; i.e., the crests of one beam falls on the troughs of the other in the center of the intersection region.
Now suppose that we keep an electron detector at the location marked by the circle. Since the two waves cancel out here, this detector will detect no electrons.
By contrast, if electrons were particles (i.e. not waves), then there would be no such cancellation, and the detector would pick up particles form both beams.
This difference is the essence of the wave nature of the electron. To prove that the electron is a wave, we set up an experiment analogous to Fig.1c, and check that the detector in the center indeed picks up no particles.

Fig.1a: A wave moving right
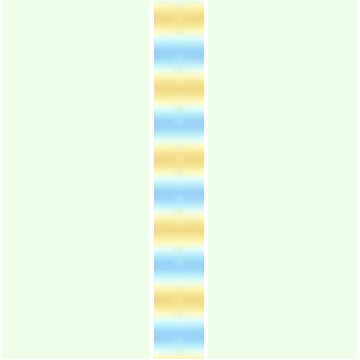
Fig.1b: A wave moving up
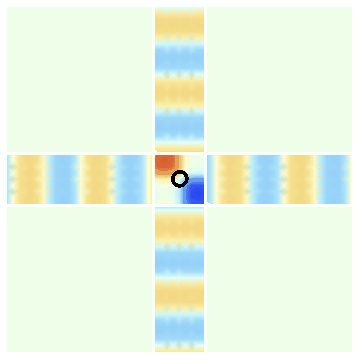
Fig.1c: Both waves present together. The waves cancel at the center. If these are electron waves, an electron detector kept at this center will detect no electrons.