Decaying the resonances manually
Resonances produce pions
Naturally, at AGS energies and above, non-stable resonances play a big role in
particle production. RQMD itself decays some of these resonances, but not all.
Especially important for pion production are the weak decays of the Lambda and
Sigma, and also the phi and the eta, all of which are still around at the
end of the RQMD calculation and so must be decayed manually;
there are even some Deltas around at the end of the calculation (see
plots of the final RQMD yields for details).
Must manually decay resonances that are un-decayed at the output of RQMD
Going through all the possible decay chains that can lead to negative pions, I find
that I must follow the following decays. There are
27 decays (some of which lead to more unstable particles which must be decayed) from RQMD which can
lead eventually to negative pions. Some particles (e.g. X-)
can lead to two pions in their decay chain.
Yadda-yadda-yadda... So who cares???
You might think that since a lot of these are weak decays, then they would decay outside the TPC,
or, even if they decayed inside the TPC, we would not count them as "primaries" (i.e. we would remove
them with the DCA cut).
But... if I only select those that decay within the TPC and would give a DCA less than 2.5 cm,
I find that half of the manually-decay product pions pass these criteria. Since
I would put those into my experimental HBT analysis, I must include them in my RQMD HBT analysis.
(Many thanks to John Sullivan of NA44 who emphasised this to me.)
Those manual-decay product pions that make the cut turn out to be about 10% of the total pions that
go into the RQMD HBT analysis. Importantly, they (1) are somewhat concentrated at midrapidity, and
(2) have a longer freeze-out distance and time than pions coming directly from collisions. This second
point means that accounting for these guys reduces significantly the value of the correlation function
at Q=0 MeV/c (the l parameter in a Gaussian parametrization).
So, what is the effect on the correlation functions? As an initial check, I used the code of
Scott Pratt to calculate the correlation function
with and without the pions from my manual decays.
Caviat: before I start concentrating on Coulomb complications,
I told his code to use the
p0-p0 wavefunction
to generate the correlation.
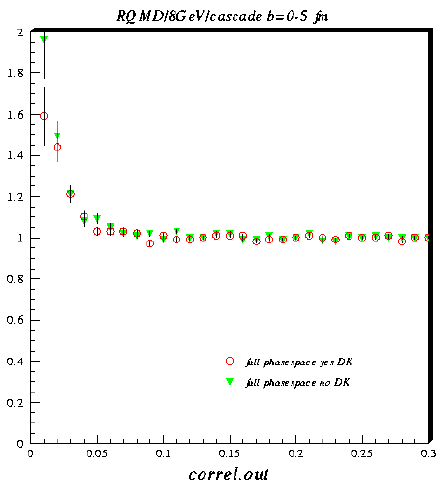 Above is shown the correlation function for RQMD at 8 AGeV in cascade mode with no phasespace cuts.
Above is shown the correlation function for RQMD at 8 AGeV in cascade mode with no phasespace cuts.
The red symbols show the correlation function when pions from my manual
decays are accounted for.
The green symbols show the correlation function when pions from my manual
decays are not accounted for.
The difference is not huge integrated over all phase space.
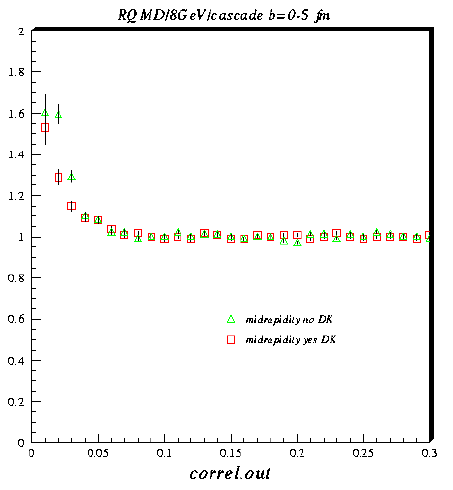 Above is shown the correlation function for RQMD at 8 AGeV in cascade mode with the cut y=1.222-1.722
(1/2 unit of y about ycm).
Above is shown the correlation function for RQMD at 8 AGeV in cascade mode with the cut y=1.222-1.722
(1/2 unit of y about ycm).
The red symbols show the correlation function when pions from my manual
decays are accounted for.
The green symbols show the correlation function when pions from my manual
decays are not accounted for.
The difference is quite significant here.
Note also that either way, the correlation is suppressed at midrapidity as compared to full phase
space coverage due to the increased percentage of pions from resonances that are
decayed by RQMD.
Back to E895 HBT and RQMD
lisa@mps.ohio-state.edu


